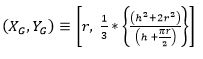CENTER
OF GRAVITY OF TWO DISTINCT SHAPES PT2
INTRODUCTION
The
center of gravity COG of an object is the point of action of the gravitational
force. It is also known as the balancing point since all objects [simple or
complex] have their COG within the object’s sphere of influence and this
ensures stability. There are two values to be noted which is the geometrical
center of gravity and the actual center of gravity. The geometrical COG is the
exact center of the object. It can be calculated by various available methods
like summation, moment of inertia, etc. The geometrical COG is valid as long as
there is uniform distribution of mass and or uniform gravitational field. In
case of uneven mass distribution or use of composite or heterogeneous
materials, the actual COG will no longer coincide with the geometrical COG.
This is because mass is distributed unevenly and the COG will shift where there
is more mass. In this article we intend to determine the COG of an assembly of
an isosceles triangle and a semi-circle.
ASSUMPTIONS
1. Mass
of the object is evenly distributed
2. The gravitational field
is uniform
3. The semi-circle
accurately fits inside the triangle
CALCULATION
Consider
a semi-circle inscribed in an isosceles triangle such that the diameter of the semi-circle
coincides with the base of the isosceles triangle. This orientation is
represented in figure.1. The triangle has height ‘h’, side length ‘b’ and base
‘a’. The diameter of the semi-circle is connected to the base of the triangle,
hence the diameter is ‘a’ and thereby the radius is ‘a/2’ or ‘r’ where r = a/2
 |
| Fig .1 Triangle and semi-circle |
We
will determine the center of gravity using the area moment of inertia method. We
need to follow four steps:
1 1. Determine the distance between the x coordinate of
C.O.G. of (triangle and semi-circle) and reference Y axis.
2 2. Determine the distance between the y coordinate of
C.O.G. of (triangle and semi-circle) and reference X axis.
3 3. Determine the area of two objects in question.
4 4. Use the Summation equation to determine the C.O.G.
coordinates.
It
is evident that the assembly represented in figure.1 is symmetric about y axis,
hence x coordinates of both triangle and semi-circle will be their midpoint.
The y coordinates are same for isosceles triangle and semi-circle.
The
coordinates and areas of triangle and semi-circle are as follows
Isosceles
triangle
X1
= r, Y1 = h/3
A1
= (1/2)*2r*h = h*r
Semi-circle
X2
= r, Y2 = 4r/3π
A2
= (1/2)*π*r2 = πr2/2
Center of gravity
The
center of gravity coordinates x and y of the assembly can be computed by using
the formula,
Negative
sign in above equations indicate that the second part (semi-circle) is being
subtracted from the whole assembly.
CONCLUSION
Thus
the center of gravity of the given assembly is located at