HIGHER RESOLUTION OCTAVE BANDS
Introduction
The word ‘octave’ is
derived from the Latin word meaning ‘eight’. In the musical world where there
are 7 notes, the 8th note sounds twice as high as the 1st
note. The 8th note is an octave higher than the 1st note.
Similarly in the octave band, the upper limit frequency is twice the lower
limit frequency. Octave bands are very useful in engineering applications
because they reveal the spectral content, meaning they represent the change in
noise levels with respect to the frequency of sound. This helps in identifying
which frequency is responsible for the noise which helps in nailing down the
component in a machine responsible for the frequency.
Octave 1/6th,
Octave 1/12th and Octave 1/24th are examples of higher
resolution octave bands. They are similar to the octave 1/1 band except that
the spectral resolution is exorbitantly high. Octave 1/6th band is
similar to octave 1/1 band but each frequency band is divided equally into 6
parts, 12 parts for Octave 1/12th band and 24 parts for Octave 1/24th
band. This increases the frequency resolution to an extent that pointing out
tonal frequencies becomes easier but at the expense of large processing times
and data consumption.
Octave
1/6th Band
 |
| Fig .1 1/6th Octave Band |
Equations
The relation between
the next and the previous center frequency is given by,
n = 6 for 1/6th
octave band
n = 12 for 1/12th
octave band
n = 24 for 1/24th
oc1tave band
CF – center
frequency
CFnext –
next center frequency
CFprev –
previous center frequency
In case of 1/6th
Octave band, the next center frequency is 1.12 times the previous. This ratio
decreases with increasing spectral resolution. The ratio is 1.06 for 1/12th
Octave band and 1.03 for 1/24th Octave band.
The relation between
the upper band and lower band frequency limit for a given frequency band is
given by,
CL – lower
band limit for a given center frequency
CU – upper
band limit for a given center frequency
n = 6 for Octave 1/6th
band
n = 12 for Octave 1/12th
band
n = 24 for Octave 1/24th
band
As the spectral
resolution keeps increasing or in other words when ‘n’ increases, the number of
upper and lower bands also increases.
Visual Representation
The picture below
explains how one band of Octave1/1 is divided into 6 equal parts for Octave 1/6
bands. The center frequencies of Octave 1/6 bands are calculated and mentioned
in the table below. The corresponding Octave 1/1 center frequencies are also
highlighted for understanding the relationship between the two.
 |
| Fig .2 Formation of Octave 1/6th band from Octave 1/1 band |
Tabular column
Octave 1/6 band
|
Center frequency
|
Corresponding Octave
1/1 band
|
Hz
|
||
Band1
|
16
|
Band1
|
Band2
|
17.95939277
|
|
Band3
|
20.1587368
|
|
Band4
|
22.627417
|
|
Band5
|
25.39841683
|
|
Band6
|
28.50875898
|
|
Band7
|
32
|
Band2
|
Band8
|
35.91878555
|
|
Band9
|
40.3174736
|
|
Band10
|
45.254834
|
|
Band11
|
50.79683366
|
|
Band12
|
57.01751796
|
|
Band13
|
64
|
Band3
|
Band14
|
71.83757109
|
|
Band15
|
80.63494719
|
|
Band16
|
90.50966799
|
|
Band17
|
101.5936673
|
|
Band18
|
114.0350359
|
|
Band19
|
128
|
Band4
|
Band20
|
143.6751422
|
|
Band21
|
161.2698944
|
|
Band22
|
181.019336
|
|
Band23
|
203.1873347
|
|
Band24
|
228.0700718
|
|
Band25
|
256
|
Band5
|
Band26
|
287.3502844
|
|
Band27
|
322.5397888
|
|
Band28
|
362.038672
|
|
Band29
|
406.3746693
|
|
Band30
|
456.1401437
|
|
Band31
|
512
|
Band6
|
Band32
|
574.7005687
|
|
Band33
|
645.0795775
|
|
Band34
|
724.0773439
|
|
Band35
|
812.7493386
|
|
Band36
|
912.2802874
|
|
Band37
|
1024
|
Band7
|
Band38
|
1149.401137
|
|
Band39
|
1290.159155
|
|
Band40
|
1448.154688
|
|
Band41
|
1625.498677
|
|
Band42
|
1824.560575
|
|
Band43
|
2048
|
Band8
|
Band44
|
2298.802275
|
|
Band45
|
2580.31831
|
|
Band46
|
2896.309376
|
|
Band47
|
3250.997354
|
|
Band48
|
3649.12115
|
|
Band49
|
4096
|
Band9
|
Band50
|
4597.60455
|
|
Band51
|
5160.63662
|
|
Band52
|
5792.618751
|
|
Band53
|
6501.994709
|
|
Band54
|
7298.242299
|
|
Band55
|
8192
|
Band10
|
Band56
|
9195.2091
|
|
Band57
|
10321.27324
|
|
Band58
|
11585.2375
|
|
Band59
|
13003.98942
|
|
Band60
|
14596.4846
|
Octave
1/6 Band Real Time Analysis
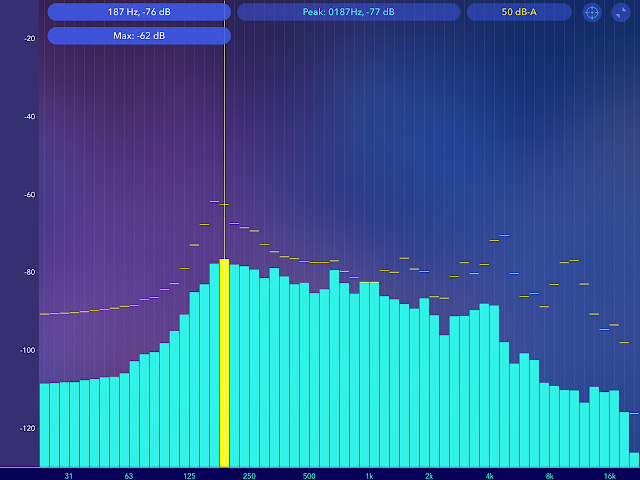 |
| Fig .3 Real time Octave 1/6th band |






