CENTER
OF GRAVITY OF A HYPERBOLIC ARC
INTRODUCTION
The
center of gravity COG of an object is the point of action of the gravitational
force. It is also known as the balancing point since all objects [simple or
complex] have their COG within the object’s sphere of influence and this
ensures stability. There are two values to be noted which is the geometrical
center of gravity and the actual center of gravity. The geometrical COG is the
exact center of the object. It can be calculated by various available methods
like summation, moment of inertia, etc. The geometrical COG is valid as long as
there is uniform distribution of mass and or uniform gravitational field. In
case of uneven mass distribution or use of composite or heterogeneous
materials, the actual COG will no longer coincide with the geometrical COG.
This is because mass is distributed unevenly and the COG will shift where there
is more mass. In this article we intend to determine the COG of a hyperbolic
arc and we assume uniform mass distribution for simplicity.
ASSUMPTIONS
1. Mass
of the object is evenly distributed
2. Earth has uniform
gravitational field
CALCULATION
Consider
a regular hyperbola. Let ‘a’ and ‘b’ be the semi major and semi minor axis of
the hyperbolic arc in consideration. The semi major axis is the distance
between the center and the vertex. The quantity ‘c’ is the linear eccentricity
which is the distance between the center and the focus. The semi minor axis is
derived from ‘c’ and ‘a’. The ratio (c/a) is the eccentricity. Consider a small
rectangular length element of width ‘dL’. This element when integrated traces
out the arc length of the Hyperbolic arc. The equation of hyperbola or arc of a
hyperbola is,
The
equation can be rearranged to represent in terms of y as,
 |
| Fig.1 Hyperbolic Arc |
To determine the center of gravity, we need to follow three steps:
1 1. Determine the length of the element in terms of one
of the known variables x or y
2 2. Determine the arc length or the total length of the
circle by integrating the element dL
3 3. Determine the C.O.G coordinates (x, y) by
integrating each variable and dividing by the total length
Once
we have the above three values, we can determine the COG coordinates.
Step1: Length of the element dL
From
fig.1, we can observe that dL can be represented in terms of ‘dx’ and ‘dy’ by
using the Pythagorean Theorem.
On
taking dx common out of the square root, we obtain
Step2: Total length of the element
We
can solve the above equation by differentiating y with respect to x, which is
differentiating the equation of circle.
On
solving we obtain,
Integrate
the above equation indefinitely to obtain the total length of the curve.
Eccentricity = sqrt{1+(b/a)^2}
The
term E[x|m] is the Elliptic integral of second kind where m = k2.
This
is the arc length of a hyperbolic arc. When the lower and upper bounds of
integration are set, we will obtain the perimeter of hyperbola or arc of
hyperbola based on the choice of limits.
Step 3: COG of the object {hyperbolic arc}
We
now can perform integral calculations to determine the x and y coordinates
respectively.
First
we integrate x and y with respect to x. Later divide each answer by ∫dL to determine the x and y coordinate of C.O.G
On
performing numerical computation, we obtain the values of integration as
follows:
The
x integral is,
The
y integral is,
The
C.O.G coordinates are,
This
simplifies to,
Where
A is,
This
simplifies to,
Where
C is,
Where
D*log(K) is,
CONCLUSION
We
thus determined the center of gravity of a Hyperbolic Arc.




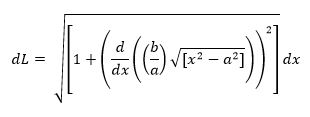
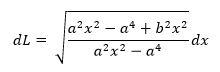











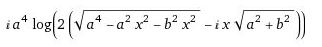
No comments:
Post a Comment