GRAVITATIONAL
FIELD LINES OF A HYPERBOLA
INTRODUCTION
The force of gravity as
described by Sir Isaac Newton is a force of attraction. The gravitational force
acting on a body of mass ‘m’ is equal to the product of its mass ‘m’ and the
acceleration due to gravity acting on that body. Now Force is a vector quantity
since it is a product of mass [scalar] and acceleration [vector]. By definition
a scalar quantity can be represented by magnitude alone whereas a vector
quantity must be represented by magnitude and direction. Thus while solving a
vector quantity, it is important to obtain both magnitude and direction to
obtain complete information of the vector. Acceleration due to gravity being a
vector quantity has both magnitude and direction. The direction of
gravitational force is termed as gravitational field lines or orthogonal
trajectories which are always orthogonal [perpendicular] to the surface as
explained in detail in the calculation section. This article intends to
determine the gravitational field lines of a hyperbolic arc or a hyperbolic
plate.
ASSUMPTIONS
1. The plate has
negligible thickness hence is assumed to be two dimensional
2. The plate is
homogeneous in nature meaning composed of only one material
3. The plate is not under
the influence of an external gravitational field
4. The whole mass of the
plate is assumed to be concentrated in the center
CALCULATION
Consider a hyperbola of
major axis ‘a’ [m], minor axis ‘b’ [m] and mass ‘m’ [Kg].
 |
| Fig .1 A hyperbola |
There is a 3 step
procedure to determine the field lines
Step1 Determine differential equation of
Hyperbola and its slope
The equation of a
regular Hyperbola with major and minor axes ‘a’ and ‘b’ is,
Rearranging the above
equation,
Differentiating equation
(2) with respect to x,
Equation (3) represents
the slope of equation (1) [Hyperbola]. Thus an orthogonal trajectory to the Hyperbola
must have a slope that is negative inverse of the slope in equation (3).
Step2 Determine the slope of the
orthogonal trajectory
Thus the new slope or
the slope of the orthogonal trajectory which is a negative inverse of equation (3)
is
Step3 Determine equation of the
orthogonal trajectory by integration
To obtain the equation
of the orthogonal trajectory, integrate equation (4) by separating the
variables. Rearranging equation (4)
{‘k’ is a constant of
integration}
Equation (5) represents
the family of orthogonal trajectories of a Hyperbola. The orthogonal
trajectories which represent hyperbolas are pictorially represented in figure
2. It is interesting to note that both ellipse and hyperbola have the same
orthogonal trajectory which is the hyperbola.
REPRESENTATION
The graph of a Hyperbola
and its orthogonal trajectories are represented in Figure 2. The hyperbolas itself
which are orthogonal trajectories to the hyperbola appear emanating outward and
perpendicular to the parent hyperbola. Thus a hyperbola or a hyperbolic plate
will have its gravitational field directed as hyperbolas.
 |
| Fig .2 Gravitational field lines of Hyperbola |
EXPLANATION
Since Hyperbola is only
symmetric about one axis x or y but not both, the gravitational field lines are
not equidistant from the center and hence the magnitude of gravitational field
is not the same at all points on the perimeter of Hyperbola. From figure 2, it
is evident that the field lines are non-uniform since they are not parallel to
each other. The non-uniformity stems from the curvature of the curve
[Hyperbola]. The field lines in general represent the direction of the field.
CONCLUSION
The final equation (5)
implies that the orthogonal trajectory of Hyperbola is family of hyperbolas. It
is important to note that the constant ‘2k’ can have infinite values hence
there are infinite orthogonal trajectories for a given shape in this case the Hyperbola.
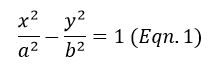





No comments:
Post a Comment