PROJECTILE MOTION ON JUPITER
INTRODUCTION
Projectile motion is a
form of motion that follows or traces out a parabolic path. The predominant
reason for the origin of projectile motion is acceleration due to gravity. When
an object is simply given a horizontal initial velocity, gravity which is always
acting downward will exert a vertical pull on the object. The resultant of
horizontal and vertical components is a parabolic motion. The magnitude of
horizontal and vertical components may or may not be equal since it depends on
the angle of trajectory. However both horizontal and vertical components are
totally independent of each other. In this post, we intend to determine time of
flight, maximum attainable height and maximum attainable distance of an object
undergoing projectile motion on the surface of Jupiter.
ASSUMPTIONS
1. Air, wind and other
frictional resistance are neglected
2. Effect of rotation of Jupiter
is negligible
3. Temperature effects do
not impede the motion
4. The ground surface is
perfectly horizontal
5. The projectile moves
along a two dimensional path
6. The projectile is
indestructible
CALCULATION
Consider an object of
mass ‘M’ kg, moving with an initial velocity ‘u’ at an angle ‘θ’ with respect
to the horizontal. Let ‘g’ be the acceleration due to gravity on Jupiter. It is
important to note that projectile motion is independent of the mass of the
object in a vacuum. However in air or other media, the drag coefficient being
different for various object shapes and sizes, it is no longer independent of
mass.
The equation of
projectile motion in this case is given by,
where,
h – Horizontal distance
at which the projectile attains maximum height (m)
k – Maximum height
attained by the projectile (m)
a – Focal length of the
parabola (m)
A projectile motion is
represented in figure.1 with all the coordinates
 |
| Fig .1 A projectile motion |
Now, the other aspects
of the parabolic motion such as total time taken, maximum height and maximum
distance attained will be discussed
The time of flight ‘T’ is
given by,
where,
T – Time of flight or
total time taken (s)
u – Initial velocity of
projectile (m/s)
θ – Angle of projectile
(degree)
g – Acceleration due to
gravity on Jupiter (24.5 m/s2)
The maximum height
attained (H) by the object is given by,
The maximum distance
attained (d) by the object is given by,
GRAPH
In order to plot the
projectile motion, substitute equations (3), (5) and (7) in equation (1) which
is the equation of the projectile motion.
Since the curve passes
through the origin, it must satisfy the origin or in other words the origin is
a trivial solution of the above equation. Thereby substituting (x, y) as (0, 0)
in the above equation, we can determine the value of the focal length which is
a constant.
Now substitute equation
(11) in equation (9) in order to plot the projectile motion.
Input the above
equation in a suitable equation or curve plotter and the corresponding result
will be obtained as shown in figure.2
 |
| Fig .2 Projectile motion on Jupiter |
CONCLUSION
Thus the time of
flight, maximum attainable height and distance of an object undergoing
parabolic motion on the surface of Jupiter were determined successfully. The
plot also verifies a proper projectile motion with the maximum attained height
and distance.





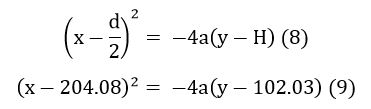


No comments:
Post a Comment