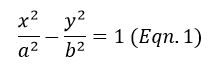- For a given polygon of side length ‘a’, the height
‘h’ will always be different for every type of polygon.
- The height ‘h’ is proportional to tangent of the
angle of the triangle. Hence ‘h’ will increase as the angle increases or in
other words ‘h’ will be greater for multi sided polygons assuming constant
length ‘a’ for every polygon.
November 6, 2022
Reasoning for distinct acceleration due to gravity on Polygons
September 24, 2022
Gravitational field lines of Hyperbola
 |
| Fig .1 A hyperbola |
 |
| Fig .2 Gravitational field lines of Hyperbola |
April 15, 2022
Gravitational field lines of Parabola
 |
| Fig .1 A parabola |
There is a 3 step procedure to determine the field lines
 |
| Fig .2 Gravitational field lines of Parabola |
January 29, 2022
X and O Privacy Policy
Privacy Policy
Effective
Date: 29-01-2022
Your
Privacy is important to us. This Privacy Policy explains how we collect, use,
disclose, and safeguard your information when you visit our mobile application
“X and O” hereinafter referred to as the “app”. Please read this Privacy Policy
carefully. IF YOU DO NOT AGREE WITH THE
TERMS OF THIS PRIVACY POLICY, PLEASE DO NOT ACCESS THE APPLICATION. We respect
your privacy and are committed to protecting personally identifiable
information you may provide us by using the app. We have adopted this privacy
policy ("Privacy Policy") to explain what information may be
collected on our app, how we use this information, and under what circumstances
we may disclose the information to third parties.
Contents
- Collection of your information
- Storage of your information
- Disclosure of your information
- Privacy Policy Changes
- Contact Information
1. Collection of your information
The
app does NOT collect any information from your device. The app does not require
any permission to be granted in order to function.
2. Storage of your information
The
app does NOT store any information on your device or on any remote server.
3. Disclosure of your information
The
app does NOT disclose any information from your device to third parties.
4. Privacy Policy Changes
We
may change this Privacy Policy from time to time in our sole discretion. We
encourage visitors to frequently check this page for any changes to this
Privacy Policy. Your continued use of the app after any change in this Privacy
Policy will constitute your acceptance of such change.
5. Contact Information
If you have any questions about our Privacy Policy, please
contact us via email at srinath6811@gmail.com
Tic Tac Toe Privacy Policy
Privacy Policy
Effective
Date: 29-01-2022
Your
Privacy is important to us. This Privacy Policy explains how we collect, use,
disclose, and safeguard your information when you visit our mobile application
“Tic Tac Toe” hereinafter referred to as the “app”. Please read this Privacy Policy
carefully. IF YOU DO NOT AGREE WITH THE
TERMS OF THIS PRIVACY POLICY, PLEASE DO NOT ACCESS THE APPLICATION. We respect
your privacy and are committed to protecting personally identifiable
information you may provide us by using the app. We have adopted this privacy
policy ("Privacy Policy") to explain what information may be
collected on our app, how we use this information, and under what circumstances
we may disclose the information to third parties.
Contents
- Collection of your information
- Storage of your information
- Disclosure of your information
- Privacy Policy Changes
- Contact Information
1. Collection of your information
The
app does NOT collect any information from your device. The app does not require
any permission to be granted in order to function.
2. Storage of your information
The
app does NOT store any information on your device or on any remote server.
3. Disclosure of your information
The
app does NOT disclose any information from your device to third parties.
4. Privacy Policy Changes
We
may change this Privacy Policy from time to time in our sole discretion. We
encourage visitors to frequently check this page for any changes to this
Privacy Policy. Your continued use of the app after any change in this Privacy
Policy will constitute your acceptance of such change.
5. Contact Information
If you have any questions about our Privacy Policy, please
contact us via email at srinath6811@gmail.com
Siren Sound Privacy Policy
Privacy Policy
Effective
Date: 29-01-2022
Your
Privacy is important to us. This Privacy Policy explains how we collect, use,
disclose, and safeguard your information when you visit our mobile application
“Siren Sound” hereinafter referred to as the “app”. Please read this Privacy Policy
carefully. IF YOU DO NOT AGREE WITH THE
TERMS OF THIS PRIVACY POLICY, PLEASE DO NOT ACCESS THE APPLICATION. We respect
your privacy and are committed to protecting personally identifiable
information you may provide us by using the app. We have adopted this privacy
policy ("Privacy Policy") to explain what information may be
collected on our app, how we use this information, and under what circumstances
we may disclose the information to third parties.
Contents
- Collection of your information
- Storage of your information
- Disclosure of your information
- Privacy Policy Changes
- Contact Information
1. Collection of your information
The
app does NOT collect any information from your device. The app does not require
any permission to be granted in order to function.
2. Storage of your information
The
app does NOT store any information on your device or on any remote server.
3. Disclosure of your information
The
app does NOT disclose any information from your device to third parties.
4. Privacy Policy Changes
We
may change this Privacy Policy from time to time in our sole discretion. We
encourage visitors to frequently check this page for any changes to this
Privacy Policy. Your continued use of the app after any change in this Privacy
Policy will constitute your acceptance of such change.
5. Contact Information
If you have any questions about our Privacy Policy, please
contact us via email at srinath6811@gmail.com
Planet Gravity Privacy Policy
Privacy Policy
Effective
Date: 03-12-2023
Your
Privacy is important to us. This Privacy Policy explains how we collect, use,
disclose, and safeguard your information when you visit our mobile application
“Planet Gravity” hereinafter referred to as the “app”. Please read this Privacy Policy
carefully. IF YOU DO NOT AGREE WITH THE
TERMS OF THIS PRIVACY POLICY, PLEASE DO NOT ACCESS THE APPLICATION. We respect
your privacy and are committed to protecting personally identifiable
information you may provide us by using the app. We have adopted this privacy
policy ("Privacy Policy") to explain what information may be
collected on our app, how we use this information, and under what circumstances
we may disclose the information to third parties.
Contents
- Collection of your information
- Storage of your information
- Disclosure of your information
- Privacy Policy Changes
- Contact Information
1. Collection of your information
The
app does NOT collect any information from your device. The app does not require
any permission to be granted in order to function.
2. Storage of your information
The
app does NOT store any information on your device or on any remote server.
3. Disclosure of your information
The
app does NOT disclose any information from your device to third parties.
4. Privacy Policy Changes
We may change this Privacy Policy from time to time in our sole discretion. We encourage visitors to frequently check this page for any changes to this Privacy Policy. Your continued use of the app after any change in this Privacy Policy will constitute your acceptance of such change.
5. Contact Information
If you have any questions about our Privacy Policy, please
contact us via email at srinath6811@gmail.com
Mantra Chanter Privacy Policy
Privacy Policy
Effective
Date: 03-12-2023
Your
Privacy is important to us. This Privacy Policy explains how we collect, use,
disclose, and safeguard your information when you visit our mobile application
“Mantra Chanter” hereinafter referred to as the “app”. Please read this Privacy Policy
carefully. IF YOU DO NOT AGREE WITH THE
TERMS OF THIS PRIVACY POLICY, PLEASE DO NOT ACCESS THE APPLICATION. We respect
your privacy and are committed to protecting personally identifiable
information you may provide us by using the app. We have adopted this privacy
policy ("Privacy Policy") to explain what information may be
collected on our app, how we use this information, and under what circumstances
we may disclose the information to third parties.
Contents
- Collection of your information
- Storage of your information
- Disclosure of your information
- Privacy Policy Changes
- Contact Information
1. Collection of your information
The
app does NOT collect any information from your device. The app does not require
any permission to be granted in order to function.
2. Storage of your information
The
app does NOT store any information on your device or on any remote server.
3. Disclosure of your information
The
app does NOT disclose any information from your device to third parties.
4. Privacy Policy Changes
We
may change this Privacy Policy from time to time in our sole discretion. We
encourage visitors to frequently check this page for any changes to this
Privacy Policy. Your continued use of the app after any change in this Privacy
Policy will constitute your acceptance of such change.
5. Contact Information
If you have any questions about our Privacy Policy, please
contact us via email at srinath6811@gmail.com