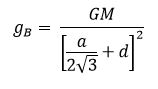Center of Gravity of a circular arc

CENTER OF GRAVITY OF A CIRCULAR ARC

INTRODUCTION

The center of gravity COG of an object is the point of action of the gravitational force. It is also known as the balancing point since all objects [simple or complex] have their COG within the object’s sphere of influence and this ensures stability. There are two values to be noted which is the geometrical center of gravity and the actual center of gravity. The geometrical COG is the exact center of the object. It can be calculated by various available methods like summation, moment of inertia, etc. The geometrical COG is valid as long as there is uniform distribution of mass and or uniform gravitational field. In case of uneven mass distribution or use of composite or heterogeneous materials, the actual COG will no longer coincide with the geometrical COG. This is because mass is distributed unevenly and the COG will shift where there is more mass. In this article we intend to determine the COG of an arc of circle and we assume uniform mass distribution for simplicity.

ASSUMPTIONS

1. Mass of the object is evenly distributed

2. The gravitational field is uniform

CALCULATION

Consider an arc of a circle. Let ‘r’ be the radius of curvature of the circle. Consider a small rectangular length element of width ‘dL’. This element when integrated traces out the arc length of arc of the circle. The equation of circle or arc of a circle is,

The equation can be rearranged to represent in terms of y as,

Fig1 Arc of a circle

To determine the center of gravity, we need to follow three steps:

1    1. Determine the length of the element in terms of one of the known variables x or y

2    2. Determine the arc length or the total length of the circle by integrating the element dL

3    3. Determine the C.O.G coordinates (x, y) by integrating each variable and dividing by the total length

Once we have the above three values, we can determine the COG coordinates.

Step1: Length of the element dL

From fig.1, we can observe that dL can be represented in terms of ‘dx’ and ‘dy’ by using the Pythagorean Theorem.

On taking dx common out of the square root, we obtain

Step2: Total length of the element

We can solve the above equation by differentiating y with respect to x, which is differentiating the equation of circle.

On solving we obtain,

Integrate the above equation indefinitely to obtain the total length of the curve.

This is the arc length of the circular arc. When the lower and upper bounds of integration are set, we will obtain the perimeter of circle or arc of circle based on the choice of limits.

Step 3: COG of the object {arc of circle}

We now can perform integral calculations to determine the x and y coordinates respectively.

First we integrate x and y with respect to x. Later divide each answer by ∫dL to determine the x and y coordinate of C.O.G

The C.O.G coordinates are,

CONCLUSION

We thus determined the center of gravity of an arc of a circle.

Gravitational Field of an Equilateral triangle plate

GRAVITATIONAL FIELD OF AN EQUILATERAL TRIANGLE PLATE

INTRODUCTION

Gravity is derived from the Latin word ‘gravitas’ meaning mass. The universal law of gravitation was coined by Sir Isaac Newton. According to the law, any two masses anywhere in the universe separated by a distance will attract each other. This force of attraction is proportional to the product of their masses and inversely proportional to square of the distance between them.

The distance between two masses can be finite or infinite, which is why gravitational force is referred to as long range force but is also the weakest force among all the other fundamental forces. All objects that have mass will attract other masses. This means that each mass has its own gravitational field just like Earth. So this implies that all objects will attract each other since they will have their own field. This is not evident on Earth since Earth’s gravitational field outweighs all other mass’s field and hence all objects no matter how massive are attracted toward the Earth. In this post we intend to determine the gravitational field of a two dimensional Equilateral Triangular plate and identify points where the plate’s own gravity is strong at some parts and weak at the other.  

ASSUMPTIONS

1. The thickness of the plate is negligible compared to its length and width.

2. The plate is not under the influence of an external gravitational field.

3. The plate is a homogeneous material.

4. All the mass is assumed to be concentrated at the center.

CALCULATION

Consider an Equilateral Triangle plate of length ‘a’ [m] and mass M [Kg]. We will first determine the center of gravity of this plate and then the magnitude of the gravitational field at points of interest.

Center of gravity

Fig1 Equilateral Triangle

The center of gravity of an Equilateral Triangle of side ‘a’ and height ‘h’ is (x,y) ≡ (a/2, h/3) ≡ [a/2, (a/2√3)]

Points of interest and their distances from center

We will consider three points namely Point A, B and D as shown in figure 1. Unlike a regular isosceles or right angled triangle, this one is an equilateral triangle, hence the distance AG must be equal to DG which will be evident from the calculations.

Point A ≡ (0, 0) or (a, 0)

The distance between Point A and C.G. can be calculated by the distance formula

Point B ≡ (a/2, 0)

The distance between Point B and C.G. can be calculated by the distance formula

Point D ≡ (b/2, h) ≡ [b/2, (√3/2)*a]

The distance between Point D and C.G. can be calculated by the distance formula

As we can observe, from the above equations, the distances AG and DG when solved are exactly the same.

Gravitational field

From Eq. 1, the force of attraction between a mass and its own surface is given by,

g = GM/R²

g – Acceleration due to gravity of the mass (m/s²)

G – Universal constant of gravitation

G = 6.67*10^-11 Nm²/Kg²

M – Mass of the object (Kg)

R – Distance between the centers of two masses (m)

Since distances AG and DG are same we will determine the gravitational field equations at points A and B.

G field at point A

The gravitational field beyond the surface is obtained by adding the additional distance,

d – Distance from the surface of the object to other object.

G field at point B

The gravitational field beyond the surface is obtained by adding the additional distance,

CONCLUSION

We thus determined the magnitude of gravitational field at various points on an Equilateral Triangle plate. We observe that gravitational field is strongest at point B and weak at points A and D. The gravitational field is exactly 4 times stronger at point B relative to the corner points like A and D. This is because point B is at a distance of h/3 from the centroid of the triangle while points A and D are located at 2h/3 from the centroid. This implies that point B is attracted more toward the center because of its closer distance than point A or point D which are far away from the center.

Arduino Flashlight Tutorial

ARDUINO FLASHLIGHT TUTORIAL

INTRODUCTION

Arduino is a microcontroller which can be programmed to do certain operations like lighting led, controlling servo, etc. This is a DIY Arduino project intended to create a flashlight (torch). Flashlights are used for general purpose in household such as alternate light source during power outage, searching in the attic, check leaking pipes, etc. A simple and inexpensive flashlight can be created by using LED’s, resistors and arduino microcontroller. The flashlight setup consists of 9 white LED’s arranged in a 3x3 matrix which are connected to the microcontroller via the resistors. The LED’s are controlled by the microcontroller which runs on the user defined code.

COMPONENTS REQUIRED

1. Perfboard and Breadboard

2. Arduino (Mega 2560 or UNO) and USB cable

3. 5mm White LED’s (9)

4. 220 Ohm resistors (9)

5. Jumpers

6. A 5V Power supply

CIRCUIT SCHEMATICS

Fig.1 Schematic

Make the appropriate connections as shown in the schematic above

CODE

This is the code for simulating a torch. Note that this code is valid only for the particular schematic represented in figure1. The values and choice of ports can always be changed. Copy and paste the code in Arduino IDE sketch area.

/*

 Arduino Torch

 9 White LED's arranged in a 3x3 grid

 220ohm resistors

Created by Srinath Srinivasan

March 3, 2019

*/

int LED1 = 2;

int LED2 = 3;

int LED3 = 4;

int LED4 = 5;

int LED5 = 6;

int LED6 = 7;

int LED7 = 8;

int LED8 = 9;

int LED9 = 10;

void setup() {

  // initialize digital pin LED_BUILTIN as an output.

  pinMode(LED1, OUTPUT);

  pinMode(LED2, OUTPUT);

  pinMode(LED3, OUTPUT);

  pinMode(LED4, OUTPUT);

  pinMode(LED5, OUTPUT);

  pinMode(LED6, OUTPUT);

  pinMode(LED7, OUTPUT);

  pinMode(LED8, OUTPUT);

  pinMode(LED9, OUTPUT);

}

// the loop function runs over and over again forever

void loop() {

  digitalWrite(LED1, HIGH);   // turn ON the LED's 1to 9 

  digitalWrite(LED2, HIGH);

  digitalWrite(LED3, HIGH);

  digitalWrite(LED4, HIGH);

  digitalWrite(LED5, HIGH);

  digitalWrite(LED6, HIGH);

  digitalWrite(LED7, HIGH);

  digitalWrite(LED8, HIGH);

  digitalWrite(LED9, HIGH);

 

                                    

}