GRAVITATIONAL FIELD OF AN EQUILATERAL
TRIANGLE PLATE
INTRODUCTION
Gravity
is derived from the Latin word ‘gravitas’ meaning mass. The universal law of
gravitation was coined by Sir Isaac Newton. According to the law, any two
masses anywhere in the universe separated by a distance will attract each
other. This force of attraction is proportional to the product of their masses
and inversely proportional to square of the distance between them.
The
distance between two masses can be finite or infinite, which is why
gravitational force is referred to as long range force but is also the weakest
force among all the other fundamental forces. All objects that have mass will
attract other masses. This means that each mass has its own gravitational field
just like Earth. So this implies that all objects will attract each other since
they will have their own field. This is not evident on Earth since Earth’s
gravitational field outweighs all other mass’s field and hence all objects no
matter how massive are attracted toward the Earth. In this post we intend to
determine the gravitational field of a two dimensional Equilateral Triangular
plate and identify points where the plate’s own gravity is strong at some parts
and weak at the other.
ASSUMPTIONS
1. The
thickness of the plate is negligible compared to its length and width.
2. The
plate is not under the influence of an external gravitational field.
3. The
plate is a homogeneous material.
4. All
the mass is assumed to be concentrated at the center.
CALCULATION
Consider
an Equilateral Triangle plate of length ‘a’ [m] and mass M [Kg]. We will first
determine the center of gravity of this plate and then the magnitude of the
gravitational field at points of interest.
Center of gravity
 |
| Fig1 Equilateral Triangle |
The center of gravity of an Equilateral Triangle of side ‘a’ and height ‘h’ is (x,y) ≡ (a/2, h/3) ≡ [a/2, (a/2√3)]
Points of interest and their
distances from center
We
will consider three points namely Point A, B and D as shown in figure 1. Unlike
a regular isosceles or right angled triangle, this one is an equilateral
triangle, hence the distance AG must be equal to DG which will be evident from
the calculations.
Point A ≡ (0, 0) or (a, 0)
The
distance between Point A and C.G. can be calculated by the distance formula
Point B ≡ (a/2, 0)
The
distance between Point B and C.G. can be calculated by the distance formula
Point D ≡ (b/2, h) ≡ [b/2, (√3/2)*a]
The
distance between Point D and C.G. can be calculated by the distance formula
As
we can observe, from the above equations, the distances AG and DG when solved
are exactly the same.
Gravitational field
From
Eq. 1, the force of attraction between a mass and its own surface is given by,
g
= GM/R2
g
– Acceleration due to gravity of the mass (m/s2)
G
– Universal constant of gravitation
G
= 6.67*10-11 Nm2/Kg2
M
– Mass of the object (Kg)
R
– Distance between the centers of two masses (m)
Since
distances AG and DG are same we will determine the gravitational field
equations at points A and B.
G field at point A
The
gravitational field beyond the surface is obtained by adding the additional
distance,
d
– Distance from the surface of the object to other object.
G field at point B
The
gravitational field beyond the surface is obtained by adding the additional
distance,
CONCLUSION
We
thus determined the magnitude of gravitational field at various points on an
Equilateral Triangle plate. We observe that gravitational field is strongest at
point B and weak at points A and D. The gravitational field is exactly 4 times
stronger at point B relative to the corner points like A and D. This is because
point B is at a distance of h/3 from the centroid of the triangle while points
A and D are located at 2h/3 from the centroid. This implies that point B is
attracted more toward the center because of its closer distance than point A or
point D which are far away from the center.








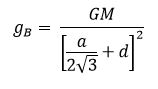
No comments:
Post a Comment